The Importance of Seeding

This post was a 2-part guest post at TeamRankings.com. Here are Part 1 and Part 2.

With a month left in the season, most of college basketball is focused on who’s in and out of the tournament. Those teams near the cut line are on the Bubble, while teams that are securely in the tournament are Locks with little worry of falling out of the bracket and seemingly little left to gain with their dance cards punched.

Turns out, there’s still plenty to play for, especially at the top. As every fan knows, the NCAA Tournament is seeded from 1 to 16 in four separate regions. The top seeds are rewarded by being placed at locations close to home, protected from a home-crowd disadvantage, and–most importantly–pitted against easier opponents. That last point is even more pronounced than one might expect. Obviously every team wants to move up a seed line, but the importance of climbing each rung of the seeding ladder might surprise.

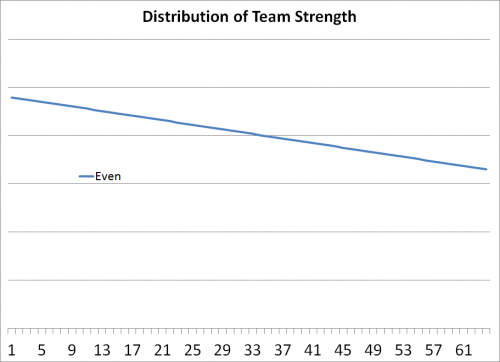
Distribution of Team Strength

Let’s assume that the quality of teams is evenly distributed such that the difference between the best team and the 2nd-best team is the same as the difference between 2nd and 3rd and between 9th and 10th and between 63rd and 64th, and so on. If we graphed that, we’d get a straight line, sloping downwards, like this:

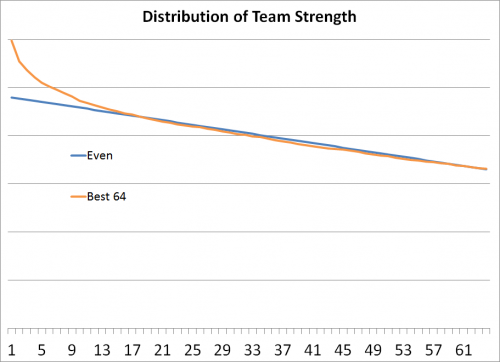
However, the teams aren’t quite distributed evenly. The best teams are a clear cut above the rest. Let’s look at how the best 64 teams are actually distributed:

The top teams increasingly put more room between them and the team below them, before it flattens out around the 15th-best team. What this means is that avoiding the top teams is imperative. In an even distribution, playing the #1 and #50 teams would be about the same as playing the #25 and #26 teams. However, in reality, playing the #1 and #50 teams is much more difficult due to the quality of the best teams.

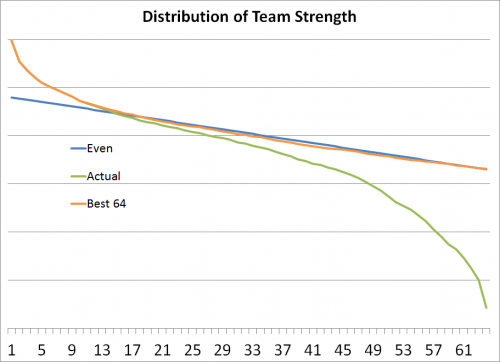
The Automatic Bids

We’re not done yet, there’s one more wrinkle and that is the NCAA policy of granting an automatic bid to each conference champion. The tournament therefore ends up with not the 64 best teams but with the best 45-50 teams and then a group of weaker conference winners.

There are actually two things going on with the green line, which graphs the actual 64 tournament teams. First, in the middle of the graph, there is a slight separation due to some of the at-large bids not going to the actual strongest teams (due to teams underachieving, or whatever the case may be). Second is the more important piece: the tail at the end of the graph is the one-bid conference automatic winners. These are the teams that occupy the 13th through 16th seed lines. I think you can see where this is going: grabbing one of those top seeds really helps a team by giving them a 1st-round game against a much weaker opponent.

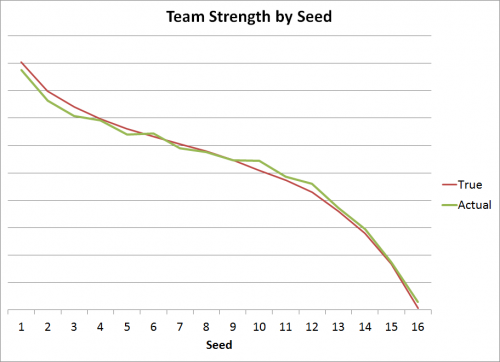
Team Strength by Seed

So we’ve identified two big reasons why seeding is not uniform: drawing the weaker automatic bids and avoiding the best teams are of increased importance. Before, we go any further, let’s look at how strong the teams at each seed line actually are. For the same reasons that we saw the slight dropoff in the green line above, teams won’t be seeded exactly according to their true strength. This will push teams somewhat towards the middle.

The red line is team strength if the seeding were “true”, meaning the 4 best teams were seeded #1, the next 4 #2, and so on. The green line, showing the average team strength by a team’s actual seed, shows a slight push towards the middle with the top seeds being a little worse than expected and the bottom seeds slightly better. However, this effect is minimal, meaning teams are generally seeded pretty close to their true strength.

Path Difficulty

Time to put it all together now. What does this all mean about a team’s chances of advancing based purely on their seed?

To determine that, I calculated a Path Difficulty for each team by looking at their potential opponents in each round, weighting by the likelihood of each opponent making it to that round (for instance, if you’re an 8-seed across from #1 seed Kentucky and #16 seed Texas Southern, both of them are potential 2nd-round opponents, but clearly Kentucky is much more likely to be your opponent), and then calculating the probability of an average tournament team winning that game.

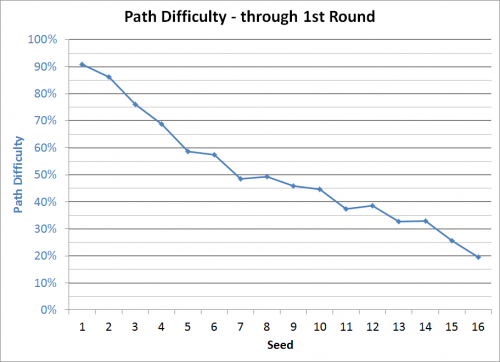
The easiest way to think about Path Difficulty through a certain round is that it is the chance of an average tournament team advancing past that round given that team’s path. Let’s start with the first round. This is pretty easy, as the only factor is your opponent. As we expect, the chart matches the previous graph of team strength by seed.

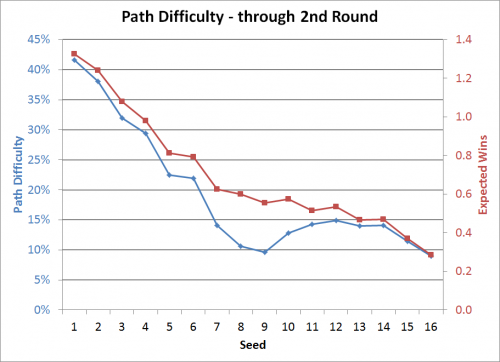
Let’s move on to the next round. The blue line is the Path Difficulty–the probability of advancing past the 2nd round–and plotted against the vertical axis on the left. The red line is the Expected Wins through the first two rounds.

The big takeaway is that in terms of reaching the Sweet 16, the only thing worse than being in the 8/9 game is being the #16 seed. As you can see with the blue line, being the 8, 9, or 16 seed all give similar chances of winning your first two games as you basically have to beat the #1 seed and either the #8 or #9 seed. However, many teams will value winning one game, so the order of playing those games matter. The red line reflects this as the 8 and 9 seeds don’t have to play the #1 seed until the second round, so their expected wins is higher.

Again, we also see the benefit of receiving a top seed. An average tournament team would be over 40% likely to make the Sweet 16 as a #1 seed, over 10% higher than even a #3 seed and nearly double the chances compared to being a typical #5 seed. From the 7-seed up, team should be fighting to climb the seeding ladder, but as we see, teams would actually increase their Sweet 16 chances as a 10-15 seed than an 8 or 9.

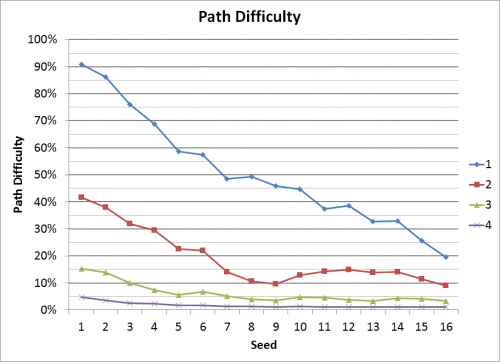
Here’s the Path Difficulty of all 4 rounds plotted together. By the 3rd round, the 8/9 and 12/13 seeds have similar paths as they have to beat the #1 seed and the #4 or #5. All of these seeds have more difficult paths than the 7/10/11/14 seeds. Their path is easier since the #2 and #3 seeds are not just worse teams combined than the #1 and #4/5 seeds, but also more likely to be upset giving an even easier matchup in the later rounds.

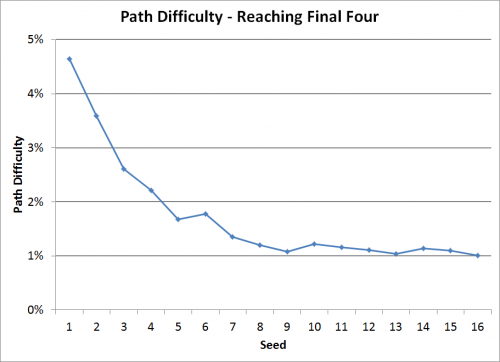
The purple line represents the Path Difficulty through the first four rounds, or, in other words, the chance of reaching the Final Four. Since all of these paths are difficult, they are dwarfed on the graph when compared to the other rounds. But focus in on just the odds of making the Final Four and we see the huge advantage for the top seeds.

Conclusion

All of this analysis was independent of the quality of the team. Obviously the better seeds are given to better teams, but this allows us to try and isolate how much of the advantage is due to seeding and not just being a better team. As we can see, the advantage is significant. Playing the weak champions of one-bid leagues in the 1st round gives top seeds a near-automatic win. Avoiding the other top teams until the later rounds–where you may even luck out and face a weaker opponent due to an upset–is another major benefit.

All those teams out there that are considered Locks, time to step up your game. Now’s the time to really bolster your NCAA Tournament chances by improving your seeding. Just stay out of that 8/9 matchup.