I’m on record many times as being in favor of a purely objective selection criteria. However, when it comes to seeding, things are a bit trickier. While selection is a purely binary process–you’re either in or you’re out–all teams are intertwined when it comes to seeding.
I’ve previously offered up an alternative where teams are selected by their resume, but seeded by their true strength. While this balances the bracket correctly, it completely abandons the reward-based nature of the tournament, which we’d like to preserve as much as possible.
There is no system to both perfectly reward teams for their body of work and preserve the integrity of the bracket so that higher-seeded teams are never given a tougher draw than a team seeded lower than them. Every time you move a team to help with bracket integrity for one team, you by definition hurt another.
Despite this impediment to perfection, we can do better than either a purely reward-based or a purely quality-based seeding system. It necessarily involves trade offs, and you have to balance maintaining the reward for some teams against hurting/helping others.
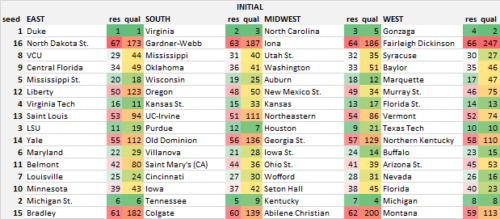
Let’s use this year’s tournament as an example throughout, though I will refer to the committee’s 1 through 68 “seed list” that they released, as opposed to the team’s actual seed they ended up with, which sometimes is adjusted up or down to preserve certain bracketing principles. I will refer to two sets of rankings for a team–one is their s-curve ranking or their resume ranking, this is the aforementioned seed list from the committee which will represent their “deserved” ranking; the other is their true strength or team quality ranking, which is a predictive measure of how good of a team they are.
Let’s start with an example (ignoring the First Four games): Duke is the #1 overall team and they drew North Dakota St. (assuming they win their play-in game versus NC Central). The Bison, however, are not the worst team in the field as the 173rd-ranked team in true strength–that distinction belongs to Fairleigh Dickinson (I’m ignoring the First Four games, so I’ve only kept the higher-quality team from each of those four games). Now, this properly rewards FDU, who the committee ranked 66th on the s-curve, one spot above NDSU, by giving them the easier matchup. However, it ends up hurting Duke, by giving them a tougher opponent. So we have a choice to make–leave it as is, or swap FDU and NDSU which will benefit Duke, but hurt FDU. Which should we do?
My philosophy is that we should generally lean towards helping the better-ranked resume team. This means that teams toward the bottom of the bracket will be seeded more by their true strength than their resume, in order to help maintain the reward for the teams with the best resumes.
The Hybrid Seeding System
Here’s how my proposal works. Certain aspects can be tweaked to slide the scale between maintaining the rewards among all teams. For example, on one end of the spectrum, you could give the #1 seed the best possible path no matter what, even if it meant moving a team down multiple seed lines, while on the other end would be a bracket seeded purely by resume. Regardless, the framework is the same.
1st Round matchups
For 1st Round matchups, the 1 through 8 seeds (top 32 on the s-curve) don’t move, but the 9 through 16 seeds are sorted based on their true strength. I did add one safeguard to help lower-seeded teams–no team can move down more than 3 seed lines. So, technically what I do is (1) take the 13 through 16 seeds, (2) take the 4 worst predictive teams and make them 16 seeds, (3) take the remaining 12 teams, add in the original 12 seeds, and repeat the process. I do this all the way up to the 9 seeds.
So we now have the top 32 teams in resume order and the bottom 32 in (mostly) predictive order. We match them up, 1 vs 64, 2 vs 63, … 32 vs 33. And those matchups are now locked.
Some examples:
- Montana, a very strong 15-seed (#113 quality), moves up to the 13-seed line. Michigan instead draws Old Dominion, who is #136 in team quality.
- Liberty, a weak 12-seed (#123 quality), drops down to a 14-seed to play Texas Tech–a better matchup for the Red Raiders than #110 Northern Kentucky.
- Wisconsin, instead of drawing a very tough Oregon team (#50 in quality), gets to play #74 Vermont instead.
2nd Round matchups
For later round pairings, all previous matchups are locked and move together. This will be more apparent after I show an example, but for instance the 32 vs 33 matchup from the 1st round starts as an 8-seed vs 9-seed matchup. If those teams get moved, they will still play each other in the 1st round, though it may ultimately be as a 7/10 matchup instead of an 8/9.
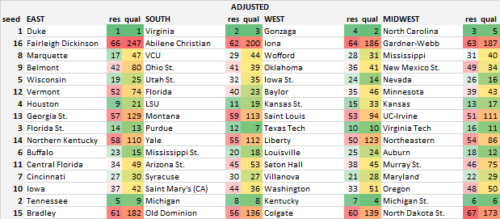
We’re now down to 32 pairings, or “pods” as I’ll call them going forward. We want to match those pods up for who will meet in the 2nd Round. So, for instance, we know Duke/FDU is in the top left part of our bracket, and we need to determine which pod will be the 8/9 matchup in their region. I just repeat a similar process as for 1st round matchups, but with a couple tweaks. First, I take the top 16 teams in the original s-curve, and they (and their 1st round matchup) remain unchanged. The other 16 pods are now sorted by the strength of their entire pod (NOTE: for the purposes of this post, I simplified things by just looking at the “best”/highest true strength team in the pod, but technically, I should calculate the weighted average of who will come out of each pod) and matched up in reverse order with the top 16 pods. So Duke, our #1 overall team, will get the weakest 2nd round pairing, whether it started as an 8/9 matchup or a 5/12 or whatever. That pod now moves to Duke’s region as the 8/9 pod, in this case it is Marquette/Belmont, an original 5/12 matchup. Again, our decision is to help either Duke by giving them the preferred matchup in the 2nd round, or to protect Marquette, who earned a 5-seed. In this proposal, we choose to help the #1 resume team at the expense of the #17 resume team.
Note, however, that Marquette still maintains their easier 1st round matchup against #80 in true quality Belmont, whereas a worse-resume, better-quality team like Nevada moves up to a 5-seed (from the 7-line) but still has to play Minnesota in the 1st Round, a significantly tougher matchup as the 43rd-best team. In this way, we are able to have our cake and eat a little bit of it too. Better resume teams are protected as long as possible–top 8 seeds are protected in the 1st round, top 4 seeds in the first 2 rounds, etc.–but can still move around the bracket to protect the very top teams in later rounds.
Sweet 16 (Regional Semifinal) matchups
We now have 4-team pods, for instance the 1/16/8/9 or the 4/13/5/12 pod. For the Sweet 16, we lock the pods that include the top 8 overall teams (the 1- and 2-seeds) and sort the other 8 pods by their pod strength.
Again, we have teams moving up/down a seed line but they maintain their matchups in the first two rounds. For example, Houston had the 9th-best resume and initially drew a 3-seed but is a weaker quality team than Virginia Tech, the original #16 team on the s-curve (initially given a 4-seed). In this step, Houston is moved to the 4-seed in Duke’s bracket, while Va Tech moves to the 3-seed in UNC’s region. However, Houston still gets to play #129 Georgia State in the 1st Round and #25 Wisconsin in the 2nd Round, while Va Tech has a much tougher path with #86 Northeastern followed by #12 Auburn, so their better resume earned them an easier path to the Sweet 16.
Elite 8 (Regional Final) matchups
The process repeats itself, now holding just the 1-seed pods the same and ranking the 2-seed pods by pod strength. For example, this year, Tennessee moves down from the #5 team on the s-curve to the #8 team and their entire pod (the 2/15, 7/10, 3/14, and 6/11 seeds from the last step) is placed in Duke’s region.
Final 4 matchups
Finally, we pair the regions together to determine who meets in the Final 4. This year, we have North Carolina, the #3 overall team on the s-curve, swap places with Gonzaga, the #4 team on the original s-curve, given that Gonzaga’s pod is tougher, so Duke’s region gets paired with UNC’s region in the Final Four.
Summary
The basics of this system are that the top 8 seeds are protected in the 1st Round, the top 4 seeds are protected through the 2nd Round, the top 2 seeds are protected through the Sweet 16, etc. In almost all protected situations, teams that rank higher on the S-Curve will have a preferred path through their protected round than a team ranked lower on the S-Curve than them. However, once a team is out of protection (i.e. in later rounds), they are subject to luck of the draw and may be helped or hurt by moving around the bracket (generally, this will benefit better quality teams and hurt lesser quality teams).
Here are a couple illustrative teams so we can see how the system works:
- Tennessee is the 5th overall team on the initial S-Curve, so they are protected through the first 3 rounds. And they benefit greatly–they play #182 Bradley in the 1st Round, #30 Cincinnati/#42 Iowa in the 2nd Round, and #13 FSU/#15 Buffalo likely in the Sweet 16. However, they are no longer protected after that, and their Elite 8 opponent is #1 Duke, the toughest draw in the tournament.
- Compare Tennessee to fellow 2-seed Michigan, the 8th overall team on the initial S-Curve. Michigan is a higher-quality team than Tennessee (#8 vs #9), so they were moved to an easier region for their Elite 8 matchup, which would be against Virginia if seeding held. However, Michigan drew a 1st Round opponent that ranks almost 50 spots higher on the team quality ranks (Old Dominion #136), a tougher 2nd round matchup in #27 Syracuse, and a much tougher Sweet 16 opponent in Purdue, the 7th-highest quality team in the country. So with this system, we are able to both reward Tennessee with an easier path than Michigan through the first 3 rounds AND also reward Duke with an easier 2-seed than Virginia, which they earned as the #1 overall seed.
- Lower down the seed list, Auburn, ranked 18th on the initial s-curve, was probably not thrilled to draw #34 quality team New Mexico State, while Maryland, who ranked 4 spots lower on the s-curve at #22 drew a much easier matchup against #80 (in quality) Belmont. Here, we correct for that and Auburn gets to play #75 Murray State while Maryland has to play #50 Oregon in the 1st Round.
Comparison of Hybrid bracket to Actual bracket
The committee’s actual bracket doesn’t perfectly match their seed list, as teams can be moved around for geographic or bracketing reasons. Still, it’s close to their seed list and provides a good comparison for the adjusted hybrid bracket. Here are the two brackets, with each team listed with their resume (s-curve) rank based on the committee’s seed list (“res”) and their true team quality rank based on how strong of a team they are (“qual”).
There’s no one way to measure the quality of the bracket but one metric to use is how often a team above you on the s-curve has an easier path and a team below you has a harder path. Ideally, we want both of those numbers to be high–if they’re both 100% for every team, that means it’s a perfectly balanced bracket. Perfection isn’t attainable (unless the s-curve exactly matches the ranking of team quality), but the hybrid bracket outperforms the initial bracket by about 5%. If you weight teams higher on the s-curve more–which I argued was more important–the gap grows to over 10%.
Last post, I argued that a perfectly objective, resume-based metric was the best way to handle selection. Seeding, however, is a much more delicate and difficult problem to tackle, given the interdependence of teams in the bracket. However, I think the Hybrid version allows us to increase the fairness of the bracket and preserve the reward for most teams while still maintaining the integrity of teams earning their place on their bracket with what they actually accomplished with their body of work.

rdawsq
an1o5l
3gag5m
g1z3p5