The Achievement S-Curve

In my last post, I discussed evaluating teams based on what they accomplished (“most deserving”) versus what they are capable of (“best”). I argued that in selecting teams for the NCAA Tournament, only a team’s wins and losses–not their margin of victory, their statistics, or their “look”–should be considered against their schedule strength in order to determine which teams deserve the reward.

Today, I put my plan into action. I introduce to you the “Achievement S-Curve”. There is no margin of victory, no rebounding margin, no NBA prospects, and certainly no “eye test” where the ASC lives. The ASC doesn’t care how you won or lost, just if you won or lost. This is based solely on each team’s achievements to-date, not their future projections.

First, a disclaimer. I am NOT projecting what the NCAA Tournament field will look like. There are plenty of sites that do that already and do it well (although, when you get spotted 31 of 68 teams, it’s not all that difficult). What I am concerned with here is what the field SHOULD look like…what the committee should look at in determining who is selected and how they are seeded.

The Criteria

I’ll lay out the things I will use to measure the “achievement” of each team during the season.

• Team Wins and Losses: Self-explanatory. For each game, I’ll need whether or not the team won or lost the game. Simple enough.
• Game Location: Again, pretty simple. Was the game at home, on the road, or at a neutral site?
• Opponent Strength: Here is where my system differs from most systems in place. To measure opponent strength, I am going to use a predictive rating system. Why? Because the actual difficulty of the game is based on how good the opponent actually is. I want to measure each team’s achievements only, but to best do that, I need to know how good their opponents really are, regardless of whether or not their achievements match. That means I’m incorporating margin of victory and statistics measuring things like shooting, rebounding, etc. in determining opponent strength. To do this, I am using a predictive rating system I have developed, but you can substitute in any rating system you want, such as Ken Pomeroy’s ratings, Jeff Sagarin’s Predictor ratings, or anything else.

The Constraints

In developing this system, there are a few constraints that I believe help to create the best version of an achievement-based rating system. Incorporating all of these into one system may not be possible, but getting as close as you can get is preferred.

1. No win can hurt you and no loss can help you. You might think that this would be a generally-accepted constraint, but it is rarely the case. In the RPI, for instance, many times simply playing a good team and losing will improve your rating, while beating a weak team will lower your rating. My system will follow this simple formula: Wins = Good, Losses = Bad.
2. Given the same schedule, it shouldn’t matter which teams you beat or lost to if you end up with the same record. For example, beating Ohio State and losing to DePaul is the same as losing to Ohio State and beating DePaul. A mediocre win and good loss is the same as a good win and mediocre loss, whatever you gain by getting a “better” win, you lose by getting a “worse” loss, and vice versa.
3. This isn’t really a constraint, but ideally the number of games a team has played wouldn’t inherently help or hurt teams. You should be able to compare a team with 30 games against a team with 25 games.

The System

Okay, let’s finally put this all together. My rating system actually ends up being quite simple. For each team, I look at all of their games. For each game, I first determine the “game difficulty”, which I define as the likelihood of an average team winning or losing against the opponent at the location of the game. For example, say that Pitt is playing UConn on a neutral floor (like they did today). An average team would beat UConn on a neutral floor 5.7% of the time, and conversely, would lose 94.3% of the time. Now, I simply debit or credit Pitt based on the outcome: if Pitt wins, they are credited +.943, and if they lose, they are debited -.057 points. A win would be a big boost while a loss would only incur a small penalty, as UConn is one of the strongest teams in the nation. I do this for every game for every team and simply add up the points.

So how does this system grade on my proposed criteria and constraint lists? Well, it only uses wins and losses, while factoring in both opponent and location. A win cannot hurt you: even if you play the theoretical worst team in the world (they would have a 0.0% chance of beating an average team), a win would simply leave your rating unchanged. The same would happen for a loss against the theoretical best team in the world (100% chance of beating an average team, so a loss doesn’t deduct any points). In addition, the distribution of wins and losses cannot change the rating. Each game has a spread of exactly 1 point (in the example above, .943 + .057 = 1.00), so trading a win for a loss and a loss for a win would move your rating down 1 point, then up 1 point, for a net result of no points.

However, the system does violate the final constraint. Good teams are better than average teams, so they should be expected to win more games than they lose. That means, on average, playing a game will result in an increase to their rating. Therefore, good teams with fewer games will not look as good as similar teams that have played more games. The astute reader has probably thought that one solution could be to divide the rating by the number of games played. However, that would violate constraint #1 above. Take a team that has beaten 10 teams that average a .75 game difficulty. If that team played a game with a .65 game difficulty, even if they won, their rating would drop. So while this system isn’t ideal, I believe it satisfies the most important criteria we are looking for.

Get to the ratings already!

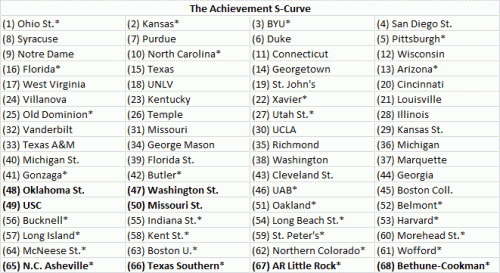
Alright, without further ado, the Achievement S-Curve. The full list of teams can be found at Google Docs here.

The teams in bold are those that would play in the First Four round: Washington St., Oklahoma St., USC, and Missouri St. would play for 12 seeds while the bottom four teams would play for the coveted 16 seeds. There are a few surprises, though overall the ASC agrees with the “bracketology” experts more than I would have guessed. On the one hand are teams higher on the ASC. Near the top, both BYU and SDSU nab 1-seeds in a close race over Pitt. UNLV is also a surprise as a 5-seed, leading me to believe that the MWC is underrated. A couple Big East teams on the downswing–Georgetown and Villanova–benefit from the full-season look. Georgetown is dealing with Chris Wright’s injury while Villanova has lost 5 straight. I disagree on both accounts: neither injuries nor “last 10 games” should be factored in. This is a full season reward. Finally, the three teams that sneak in as at-large bids that disagree with the consensus: Oklahoma St., Cleveland St., and Missouri St. In the case of the latter two, I think the consensus is underrating these team’s accomplishments simply because they play in “mid-major” conferences. Their profiles have many good wins instead of a few great wins.

On the flip side, Texas and Kentucky take a hit in the ASC. Kentucky is one of those teams that is better than what they have accomplished. Oddly enough, their partner in crime–Washington–is currently seeded correctly based on their achievements. Interesting. A couple other power conference teams that seem to be overrated take a bit of a hit here: Vanderbilt and Texas A&M.

Conclusion

The Achievement S-Curve may not be perfect, but it certainly helps to highlight where the current Bracketology thinking is going wrong. It eliminates all bias by determining the methodology first and letting the results follow. One big discrepancy comes from the “most deserving” versus “best” debate, which I have covered extensively. Even if the latter is preferred, that can be incorporated in a system like this to provide more objective results. Additionally, the committee (or at least the Bracketologists mimicking the committee) seem to be underrating some of the better mid-major conferences: the Mountain West, Horizon, and Missouri Valley. Too much emphasis is placed on “good wins” and “bad losses” without looking at how all the games left in the middle add up. Frankly, this is something that computers are simply much better at than humans. We cannot accurately assess the intricacies of a 30-game schedule, let alone 300+ 30-game schedules.

What the ASC does is provide an accurate evaluation of a team’s entire season. Did you win or lose? Who did you play? Where was the game played? The answers to those questions should be all we need. No more Top 50-RPI wins, no more sub-150 RPI losses, no more last 10 games, and certainly no more “eye test”. Let the team’s achievement on the court do the talking…you’ll just have to let the computer add it up for you.